小学5年生 算数 無料問題集 三角形の角の大きさ おかわりドリル
三角形の辺の長さの比と角の大きさには,どんな関係があるのでしょうか。 3:4:5は,斜辺の対角が直角 です。 このことは, 三平方の定理 として知られています。 3:4:5の比は,直角を作るため日常的に使われます。 その他にも,5:12:13,7:24:25直角三角形の底辺と角度から、高さ・斜辺・面積を計算します。 底辺と角度を入力し「高さ・斜辺・面積を計算」ボタンをクリックすると、入力された直角三角形の高さと斜辺と面積が表示されます。 底辺a: 角度θ: 度 ラジアン 底辺aが1、角度θが30°の直角三角形 高さ b: 斜辺 c: 面積 S: 三角形の計算 ・ 正三角形 (辺から高さと面積)
三角形 角度 出し方
三角形 角度 出し方- 三角定規の角度 三角定規は2種類の直角三角形で90°が1つ入っています。 残りの2つの角度が分かるようにします。 その1 1つ目の三角定規は正方形を半分にした直角二等辺三角形で、90°以外の角度は2つとも45°です。 座標計算の求め方 2点の座標値が器械点A (1749 7870)、視準点B (1801 )を計算する場合 直角三角形を作り、bとcの距離とθの角度を求めてみましょう。 bとcの距離は以下のようになります。 b =X2X1=5372 C =Y1Y2=997 次にθを求めてみましょう。

簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく
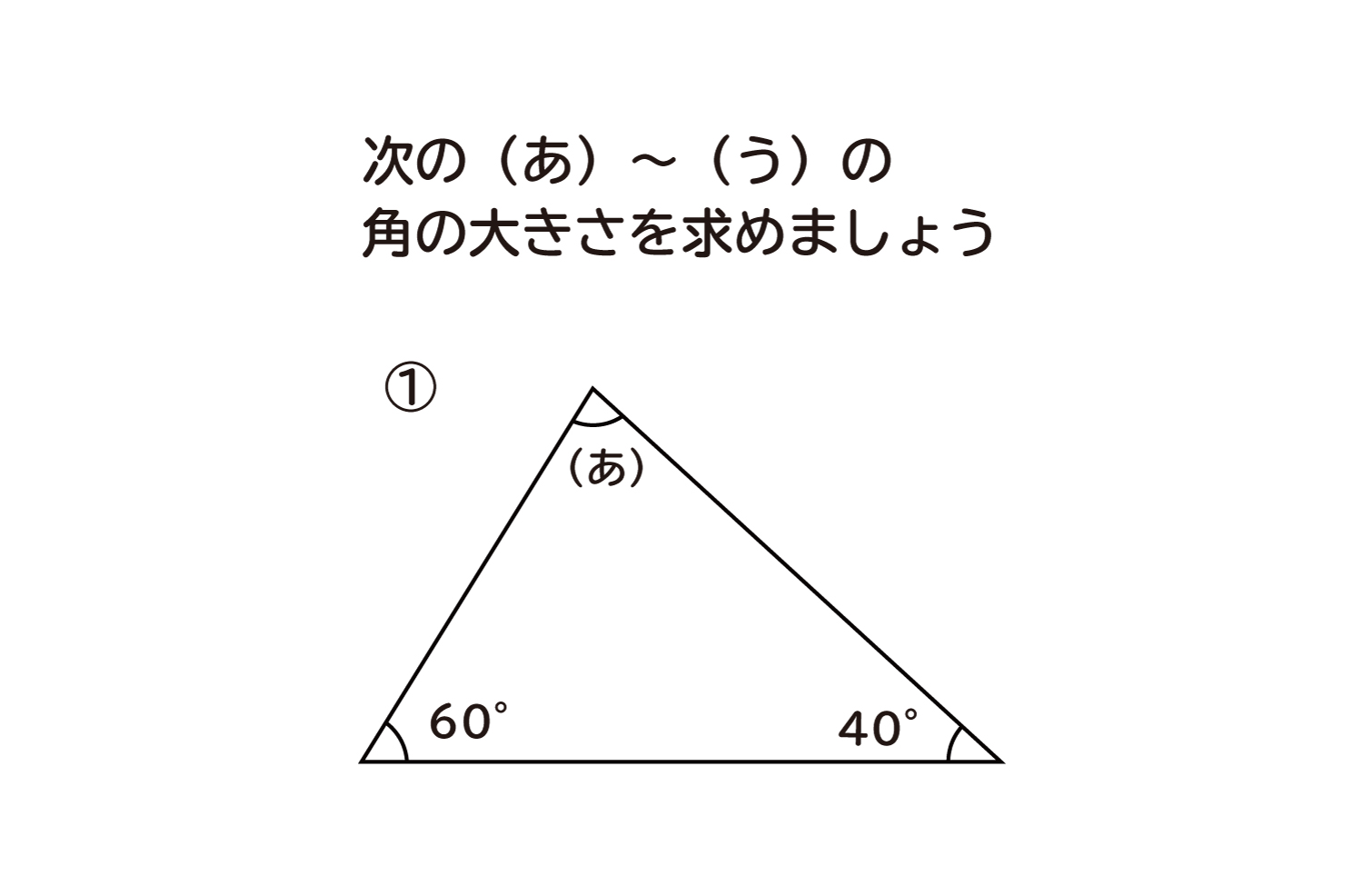
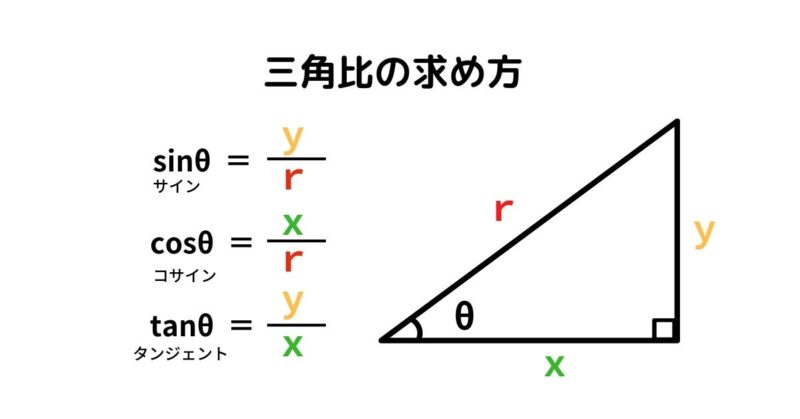
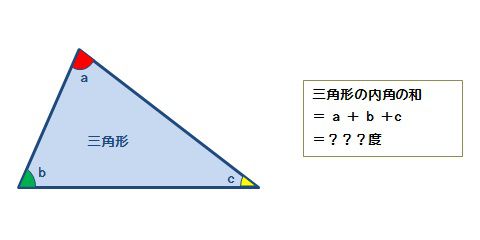
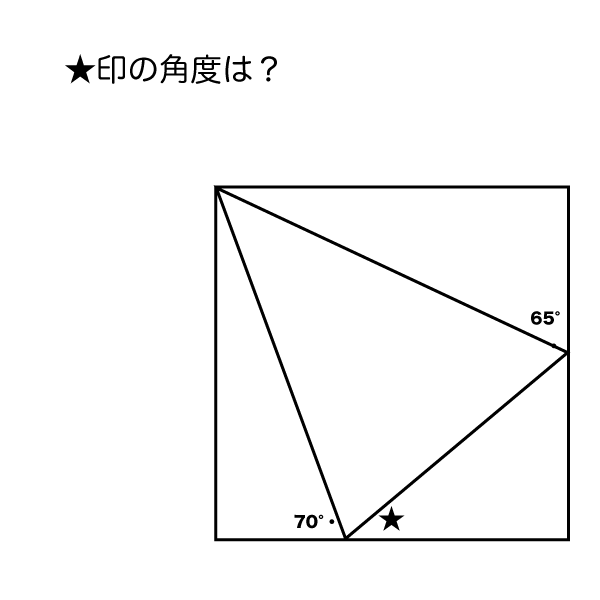
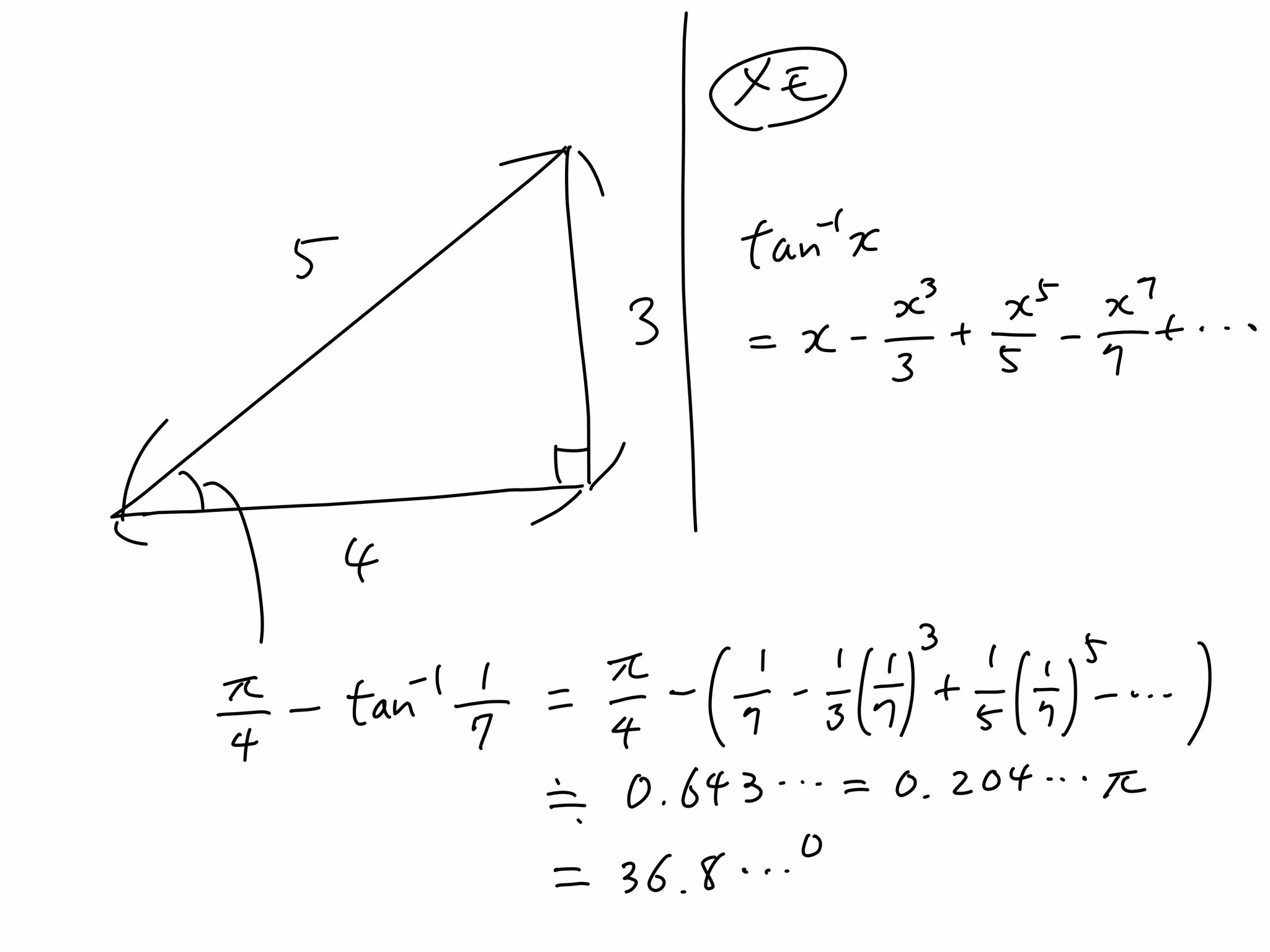
(1)三角形の内角の和と外角の定理を利用して、三角形の角の大きさを求めましょう。まず、内角と外角とは何か学んでいきましょう。 三角形の内角の和は、全ての 多角形 たかっけい の角度を求めるときの基礎です。学習する学年:中学生 1.三角比って何? 三角比とは、直角三角形の3つある角の90度以外のどちらか1つの角度が決まれば、3つの辺の長さの比率が決まるという性質のことです。 注意:直角二等辺三角形の場合は角度が決まらなくても3辺の比率は決まってしまいます。三角方程式を解いて角度を求める際は、単位円を用います。 STEP1 角度の範囲を確認する まず、求める の範囲を確認します。 今回は と設定されているので、 単位円 周分を考えます(→ 補足① 単位円と三角比の関係 )。 STEP2 条件を図示する 与えられた条件を単位円に記入しましょう。 今回は なので、 の直線を引きます。 , , の長さの感覚は、暗記した直角三角形とともに身につけておきましょ
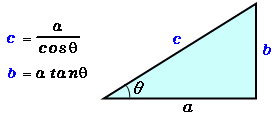
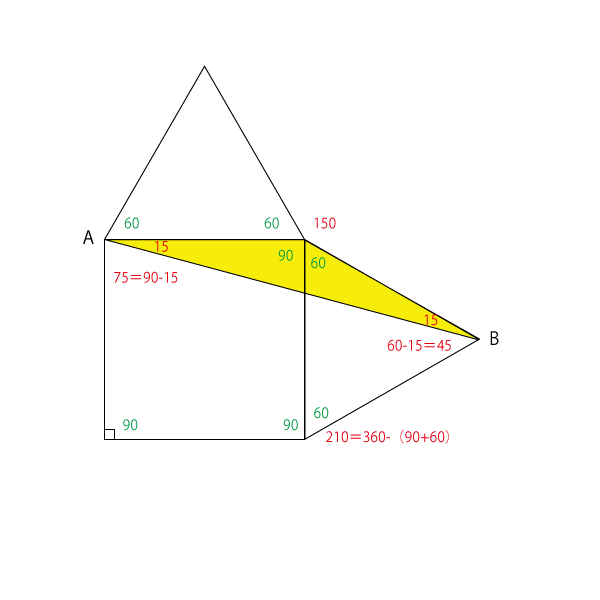
1 多角形の辺の数を数える 内角の角度を計算するには、まずその多角形がいくつの辺で構成されているのかを把握する必要があります。 多角形は辺と、辺と同数の角で構成されているということを覚えておきましょう。 例えば、三角形とは3つの辺と3つのこの2パターンの考え方がありましたが、 1°、135°、150°のように直角三角形がつくれる場合には、半径をあとから設定。 0°、90°、180°のように直角三角形がつくれない場合には、半径を1に設定。 このように使い分けていくと便利ですね! これらの考え斜面の角度は、三角形の斜辺と高さが既知であれば計算できます。下図に三角形を示しました。 斜面の角度の計算式は下記です。※値の単位はラジアンです。 θ=Asin(b/c) ラジアンの意味、度数表示の方法は下記が参考になります。
三角形 角度 出し方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 1 |  1 |  1 |
 1 |  1 | 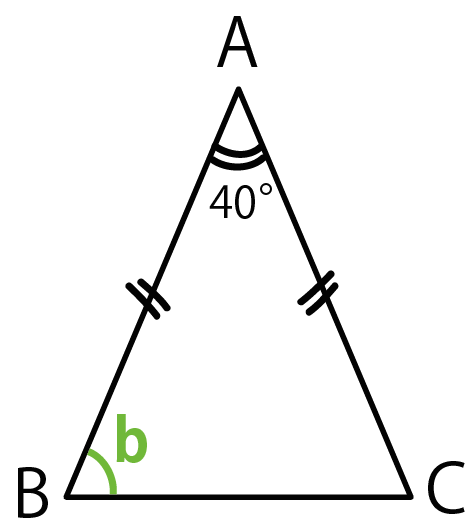 1 |
1 | 1 |  1 |
 1 | 1 | 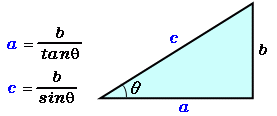 1 |
 1 | 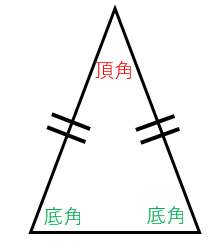 1 |  1 |
 1 | 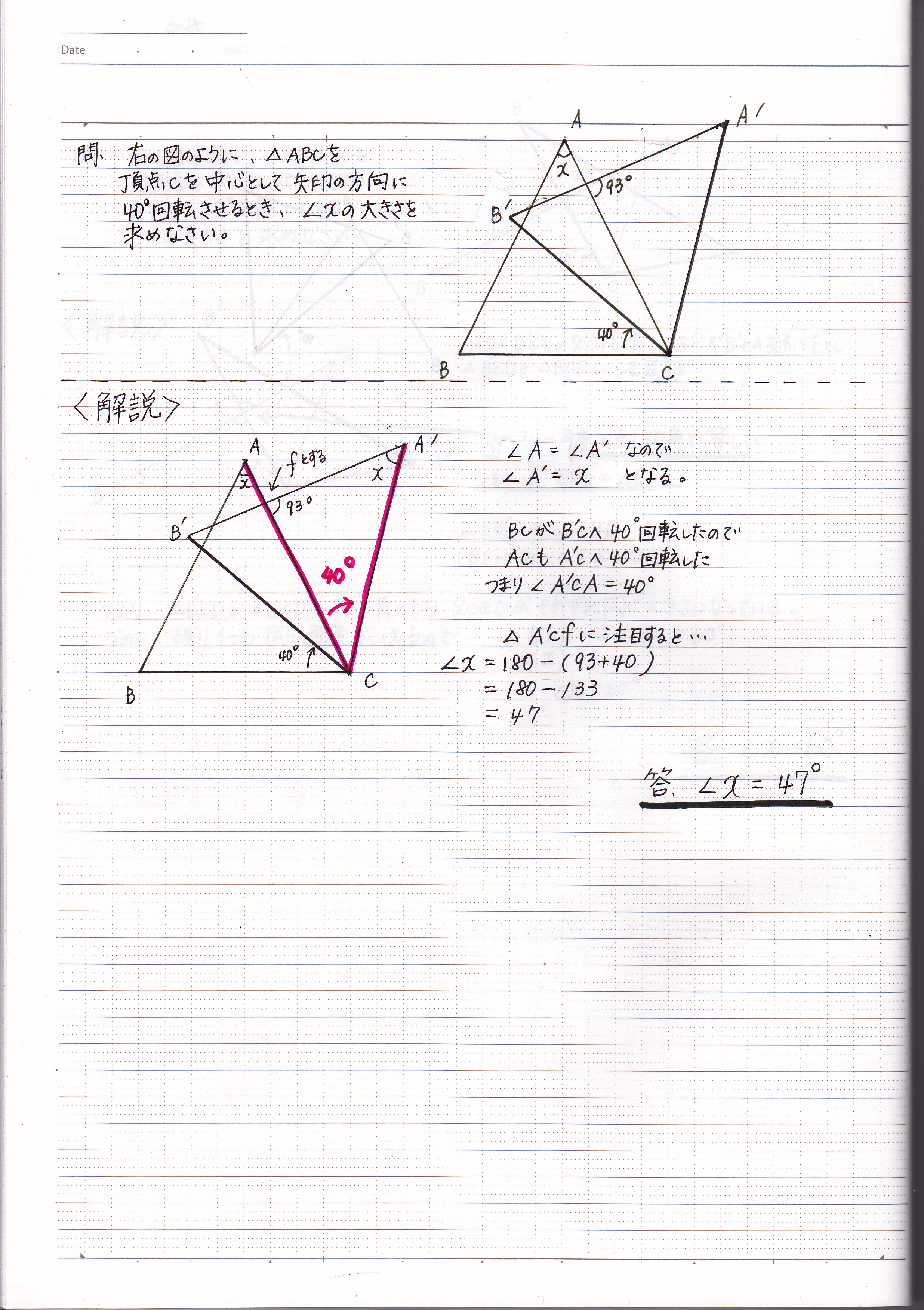 1 |  1 |
 1 |  1 |  1 |
 1 | 1 |  1 |
 1 |  1 |  1 |
 1 |  1 |  1 |
 1 |  1 | 1 |
 1 |  1 |  1 |
 1 |  1 |  1 |
 1 |  1 | 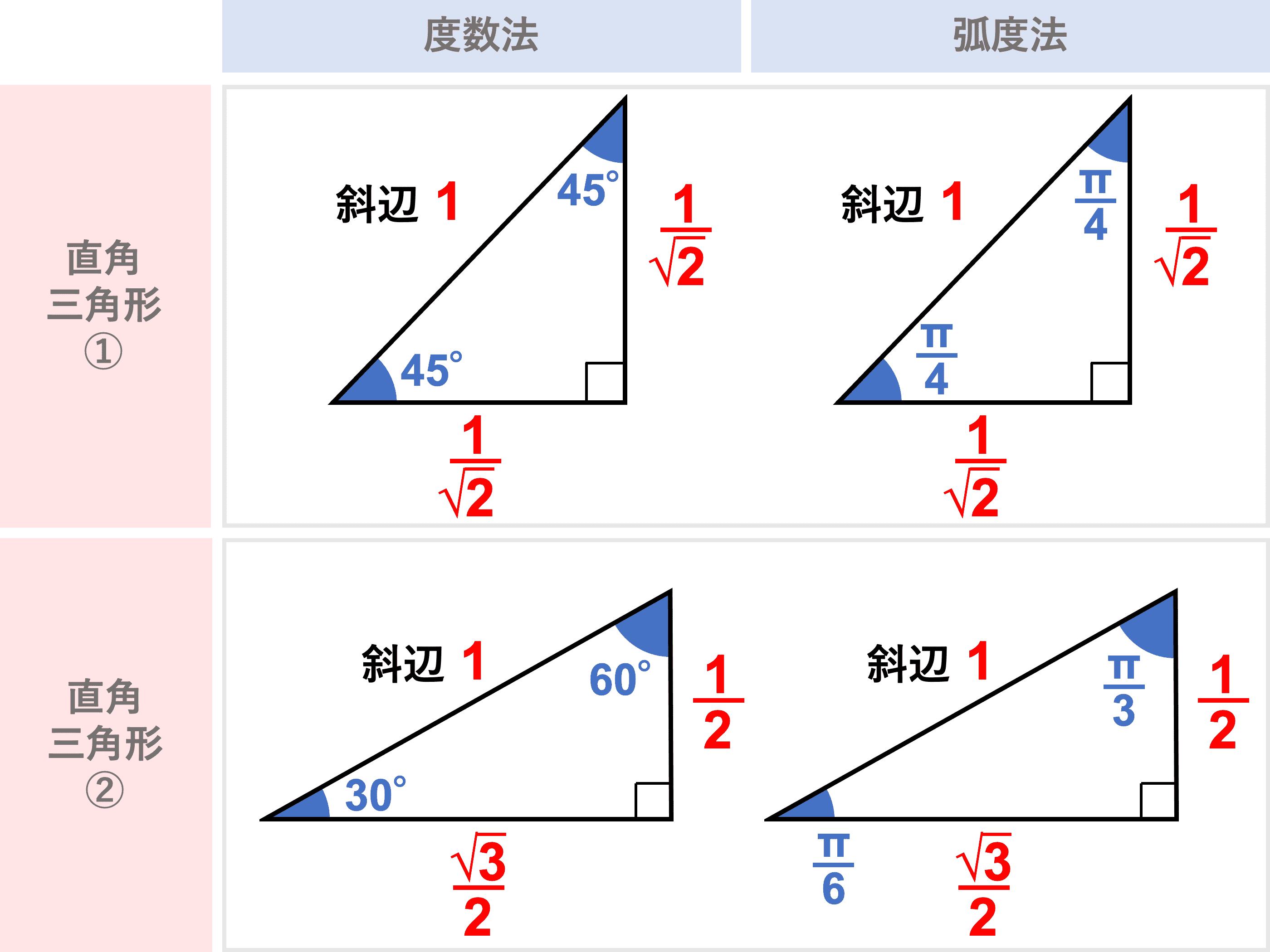 1 |
 1 |  1 |  1 |
 1 | 1 | 1 |
 1 | 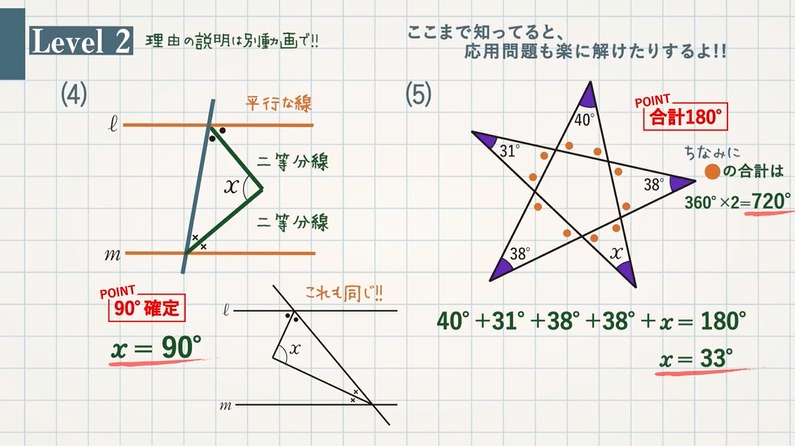 1 |  1 |
 1 | 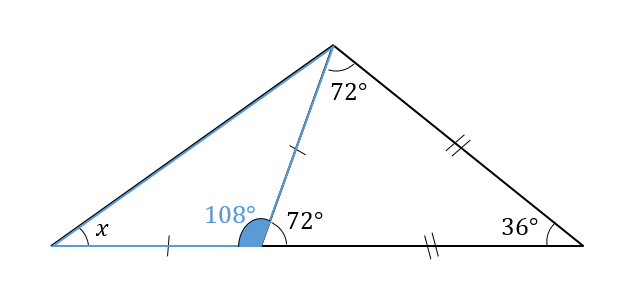 1 | 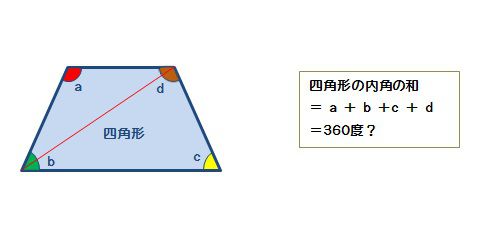 1 |
 1 | 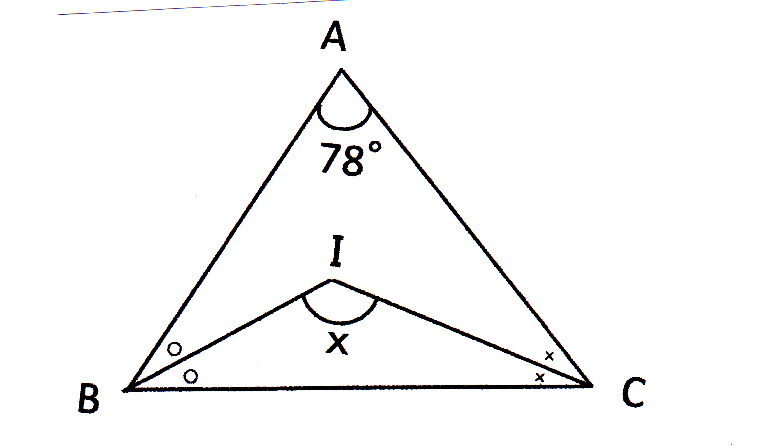 1 | 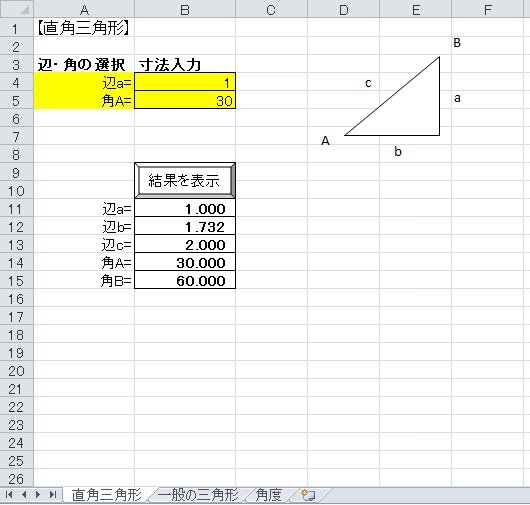 1 |
1 | 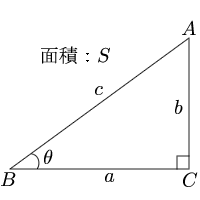 1 | 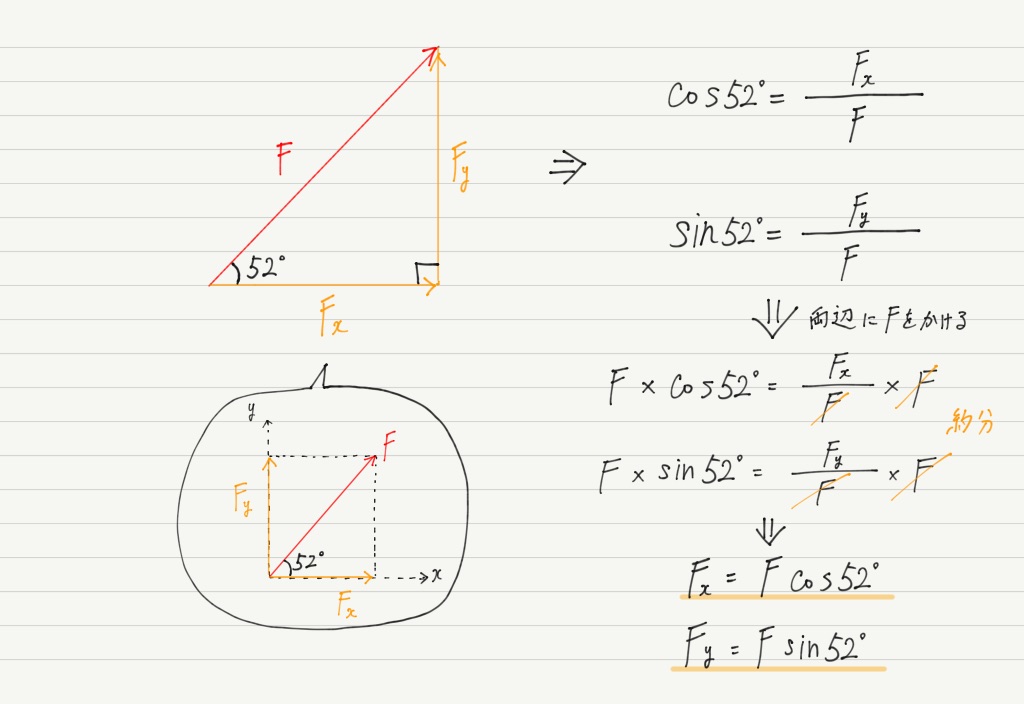 1 |
 1 | 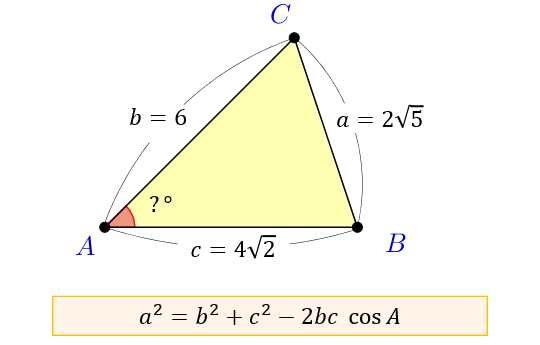 1 |  1 |
 1 | 1 | 1 |
 1 | 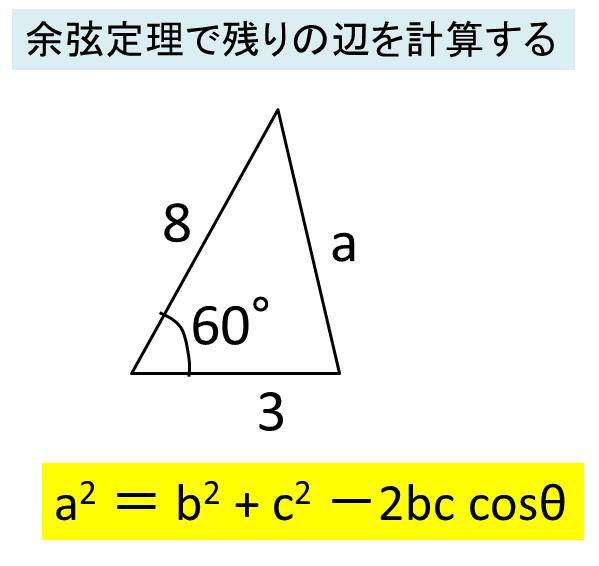 1 | 1 |
 1 |  1 | 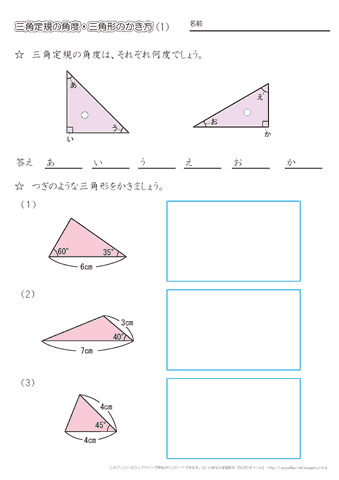 1 |
 1 | 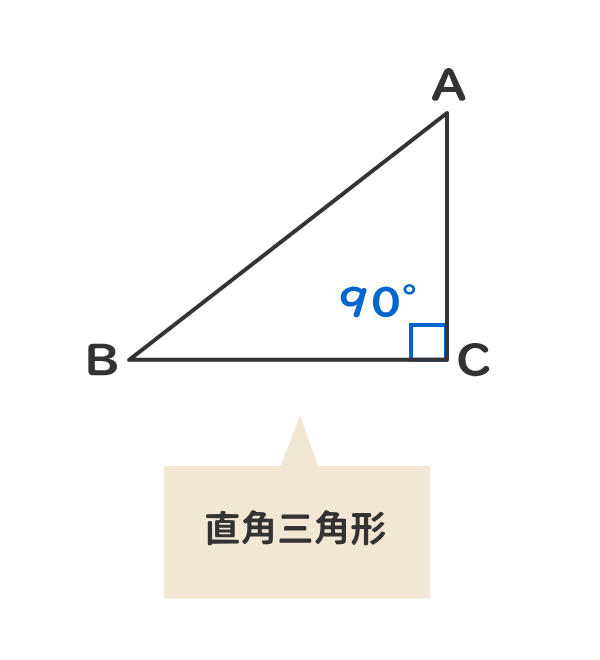 1 | 1 |
 1 |  1 |  1 |
 1 |  1 |  1 |
 1 |  1 | 1 |
1 | 1 |  1 |
 1 |  1 |  1 |
 1 |  1 |  1 |
1 | 1 |  1 |
 1 |  1 |  1 |
 1 |  1 |  1 |
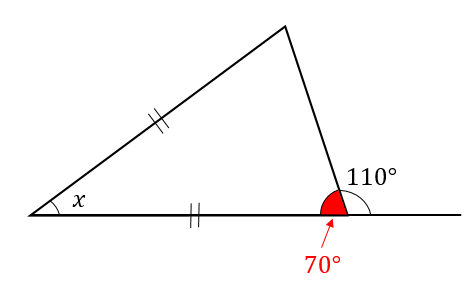
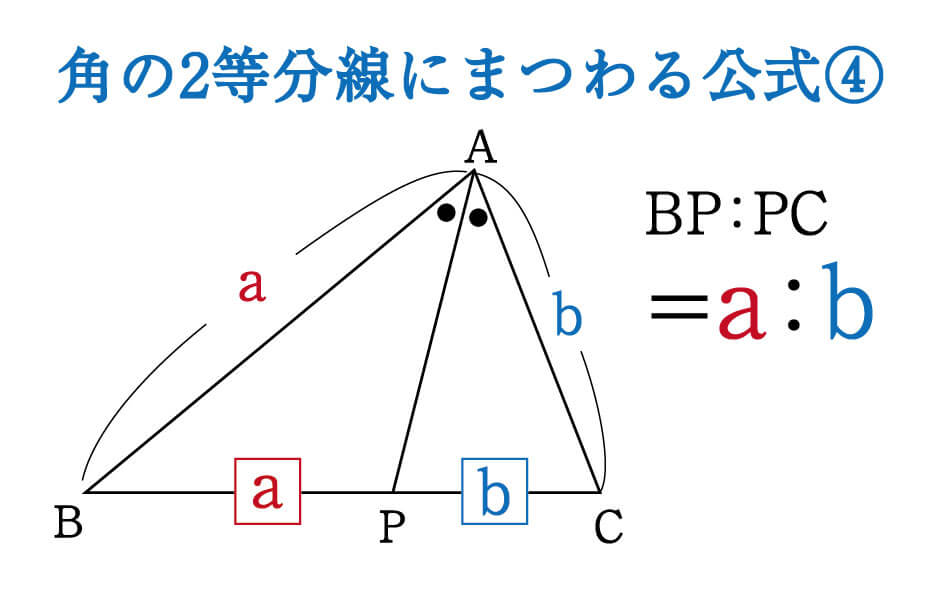
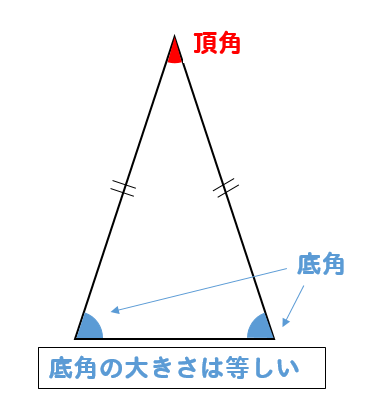
次の順番で、正三角形の角度を求められるようになります。 正三角形の角度の求め方・ 2 ステップ 1 、 1 つの内角は、 180 ∘ ÷ 3 で求める 2 、 1 つの外角は、 360 ∘ ÷ 3 で求める 正三角形の角度の求め方を見ていきましょう。 正三角形の角度と求め方 1二等辺三角形の角度の求め方 まとめ お疲れ様でした! どの問題においても、使っている性質は 『底角の大きさは等しい』 というものだけですね。 二等辺三角形が見つかったら どこが頂角で底角なのかをしっかりと把握することができれば 角度の
Incoming Term: 三角形 角度 出し方,




0 件のコメント:
コメントを投稿